免责声明：文章转载自网络，仅供行业学习交流之用，侵删。

1. 光纤的结构与类型

光纤是一种纤芯折射率n₁比包层折射率n₂高的同轴圆柱形电介质波导，如图1所示。

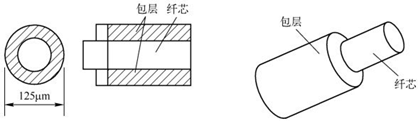
图1：光纤的结构

实用光纤的结构、折射率分布和在纤芯内的传输路径如图2所示。纤芯材料主要成分为掺杂的SiO₂，纯度达99.999%，其余成分为极少量的掺杂剂（如GeO₂等）。掺杂剂可以提高纤芯的折射率。纤芯直径为3～100μm。包层材料一般也为SiO₂，外径为125μm，其作用是把光限制在纤芯中。为了增强光纤的柔韧性、机械强度和耐老化特性，还在包层外增加一层涂覆层，其主要成分是环氧树脂和硅橡胶等高分子材料。光能量主要在纤芯中传输，包层为光的传输提供反射面和光隔离，并起到一定的机械保护作用。

根据光纤横截面上折射率的径向分布情况，把光纤可以粗略地分为阶跃型和渐变型两种。

作为信息传输波导，实用光纤有两种基本类型，即多模光纤和单模光纤。

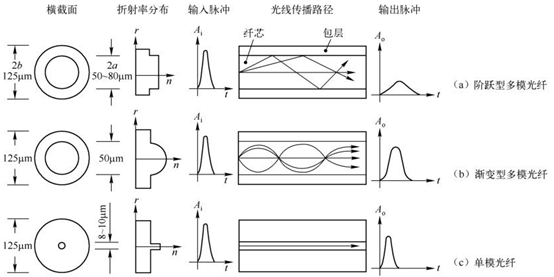
图2：实用光纤的结构、折射率分布和在纤芯内的传输路径

如图2所示，可以传播数百到上千个模式的光纤称为多模（Multi Mode，MM）光纤。根据折射率在纤芯和包层的径向分布情况，多模光纤又可分为阶跃多模光纤和渐变多模光纤。

只能传播一个模式的光纤称为单模光纤。标准单模（Single Mode，SM）光纤折射率分布和阶跃多模光纤相似，只是其纤芯直径比多模光纤小得多，其模场直径只有3～10μm，光线沿轴线直线传播。

2. 从多模光纤到单模光纤

从几何光学角度而言，光线利用全内反射沿不同的路径在多模光纤中传播。从波动光学角度而言，不同模式就相当于光走的不同路径。

光纤的横向折射率曲线一般是径向对称的，也就是说，折射率只取决于径向坐标 r而不取决于方位坐标φ。另外，几乎所有光纤（除了光子晶体光纤）的指数剖面都只表现出很小的指数对比，因此可以认为光纤是弱波导。在这种情况下，光纤模式的计算被大大简化，我们得到的是线性极化的LP模式。

这些LP模式是基于柱坐标的复电场波动方程的解。

LP模式有两个指数，第一个是方位指数，第二个表示第一个指数有多少个解，这样就有LP₀₁、LP₁₁、LP₁₂等模式。第一个指数大于1的模式是分瓣的，可能从上下或左右等不同角度分瓣。那实际上是两种互相正交的模式，但这里将其看作一种模式处理，并且将正交偏振态看成同一种模式。

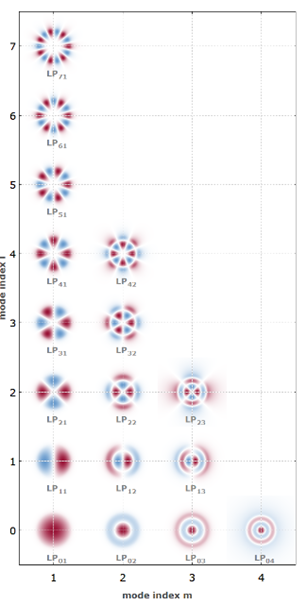
图3：LP模式

当光纤的纤芯变得越来越小（比如只有10um），我们从紫外开始逐渐增加耦合到纤芯中的波长。随着波长变长，纤芯就相对变小，因此只能容纳更少的模式，而越高阶的模式越先泄漏而不能被光纤传导。当增加到某个波长时将只剩下LP₁₁和LP₀₁两种模式。随着波长继续变长， LP₁₁模式和LP₀₁模式也先后截止，此时光纤不能传导任何光。

因此，在LP₁₁模式截至和LP₀₁模式截至的波长范围内，光纤只能传导LP₀₁模式，称为基模。

3.单模光纤的性质

（1）模场直径

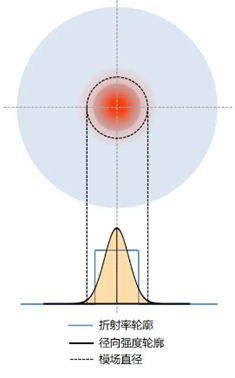
图4：模场直径

单模光纤的截面轮廓，基模略大于纤芯，稍微进入了包层。

基模强度轮廓接近高斯形，基模强度的1/e²直径叫做模场直径(MFD)。

（注意：不同厂家有不同的模场直径的定义。）

在进行光纤耦合时，模场直径可以作为有效纤芯尺寸。因为模场直径大于纤芯，虽然最高光强处于纤芯中心，但纤芯之外还有很大的强度面积，因此约有45%的光功率在包层而不是纤芯中传播。

（2）远场的输出光斑

单模光纤在远场的输出光斑是几乎完美的高斯形，没有散斑效应，并且和耦合条件无关。

单模光纤还能用于模式滤波，将混模光束耦合到单模光纤中，光纤将输出完美的高斯光束。

（3）弯曲不灵敏性

单模光纤具有弯曲不灵敏性，即受弯曲影响很小，而且输出光斑不会因弯曲而改变。

（4）无模间色散

对于单模光纤，光只能在一个模式中传播，只能沿一条路径传输，没有模间色散，从而能实现搞得数据传输速度。

（5）低衰减

单模光纤的衰减一般远低于多模光纤，这是因为光只能以LP₀₁基模传导，功率无法转移到高损耗的高阶模式中。

（6）耦合难度大

单模光纤的纤芯小，比多模纤芯小很多，这就意味着单模光纤耦合时更难实现高耦合效率，而且光纤、光束和透镜都要精确对准。

4. 单模光纤的参数

单模光纤NA一般在0.1左右，这是非常小的。

模场直径（MFD）与纤芯直径(d)、数值孔径(NA)和波长(λ)的关系为

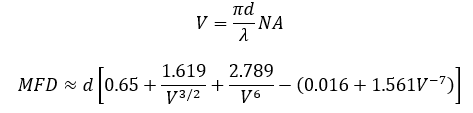
上式中，V是单模光纤的归一化频率。

V数小于2.405时，光纤只支持单模工作，截止波长的理论计算值比实际要大。

则，截止波长λ_c与纤芯直径(d)、数值孔径(NA))的关系为

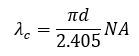
5. 单模光纤的输出

多模光纤的输出光束性质可用几何光学模拟：输出角/接收角和发生全内反射时纤芯-包层界面上的入射角有关，也和纤芯和包层的折射率差(NA)有关。

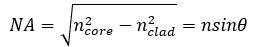
注意，上式只能计算多模光纤的NA。

单模光纤输出的是自由空间高斯光束，如果用模场直径(MFD)的一半代替自由空间光束的束腰半径(ω₀)，这样就可算出光纤输出光束的瑞利长度、任意位置的光束半径和远场发散角，如下：

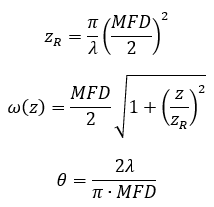
虽然单模光纤输出的远场发散角只通过波长和束腰半径计算，但NA的间接影响也值得注意。因为通过不同的NA和纤芯直径(d)组合可实现相同的截止波长，而纤芯越小，模场直径也越小，但发散角越大，因此NA也将间接地影响单模光纤输出的发散角。

6. 单模光纤的耦合

光纤的耦合效率是耦合到光纤中的功率P₁与入射光束的功率P₀之比，即

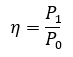
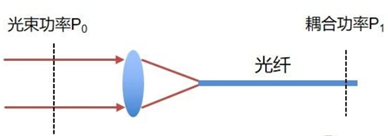
图5：光纤耦合示意图

对于单模光纤，基模可以很好地近似为高斯函数：

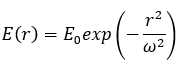
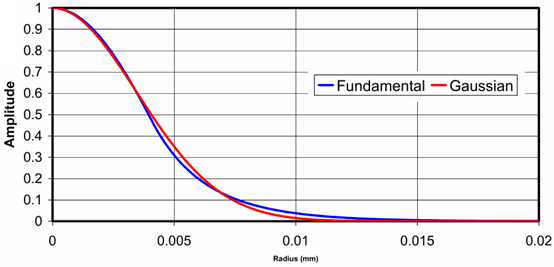
图6：单模光纤基模的高斯形

因此，耦合效率(η)在数学上定义为单模光纤模式[E₀(x,y)]与入射波[E_in (x,y)]之间的归一化复积分：

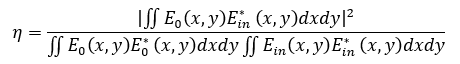
单模光纤模式的高斯近似简化了耦合效率的计算。

对于入射光束，入射光越接近高斯光，耦合效率越高。如果入射光为高斯光，其束腰在光纤端面处，且等于光纤MFD，就可以达到很高的耦合效率。

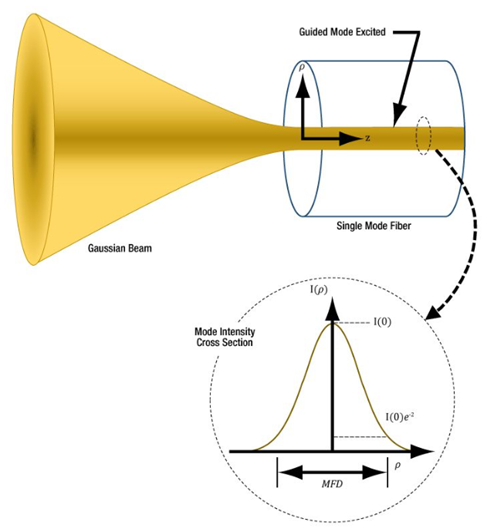
图7：单模光纤的耦合

7. 影响单模光纤耦合效率的因素

如果想使单模光纤的耦合效率最高，入射光束需要满足以下条件：

（1）入射光束接近高斯光；

（2）入射光束从光纤端面正入射；

（3）入射光束的束腰位于光纤端面；

（4）入射光束的束腰中心对准纤芯中心；

（5）入射光束的束腰直径等于单模光纤的MFD（MFD≈1.15d）。

下面讨论当以上条件不满足时，对单模光纤耦合效率的影响。

（1）模式失配损失（Mode mismatching loss）

模式失配，即入射光束的束腰直径不等于单模光纤的MFD，如图8所示。

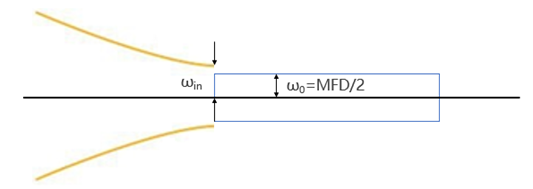
图8：模式失配

假设入射光束的束腰位于光纤端面，入射光束的束腰中心与纤芯中心对准且正入射，此时单模光纤的耦合效率为

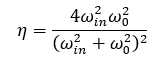
图9为SMF-28单模光纤耦合模式失配的拟合曲线。

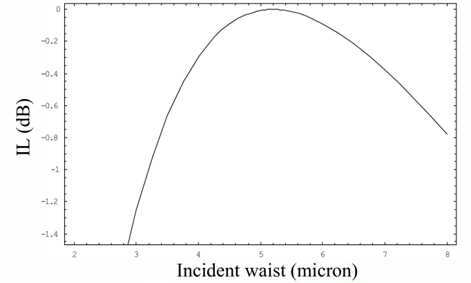
图9：模式失配的拟合曲线

（2）横向失配损失（Lateral Mismatching Loss）

横向失配，即入射光束的束腰中心没有与纤芯中心对准，如图10所示。

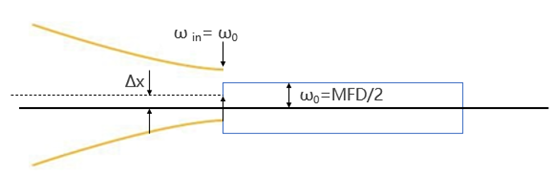
图10：横向失配

此时，假设入射光束的束腰位于光纤端面且正入射，入射光束的束腰直径等于单模光纤的MFD，但是入射光束的束腰中心与纤芯中心横向偏移Δx，此时单模光纤的耦合效率为

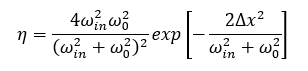
图11为SMF-28单模光纤耦合横向失配的拟合曲线。

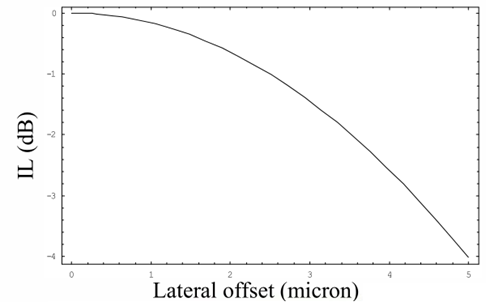
图11：横向失配的拟合曲线

（3）轴向失配损失（Longitudinal mismatching loss）

轴向失配，即入射光束的束腰中心没有位于光纤端面，如图12所示。

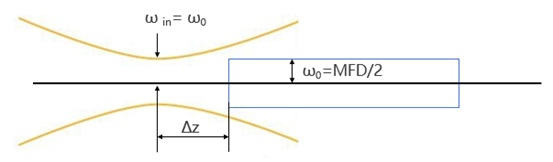
图12：轴向失配

此时，假设入射光束的束腰直径等于单模光纤的MFD，入射光束的束腰中心与纤芯中心横向对准且正入射，但是，入射光束的束腰与光纤端面轴向偏移Δz，此时单模光纤的耦合效率为

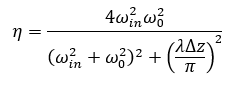
图13为SMF-28单模光纤耦合轴向失配的拟合曲线。

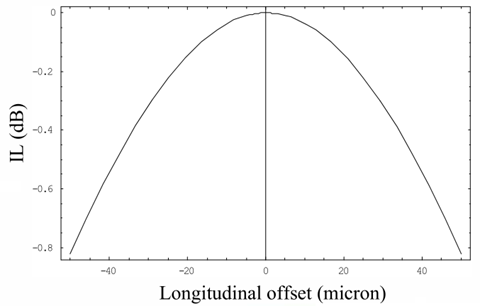
图13：轴向失配的拟合曲线

（4）角度失配损失（Angular mismatching loss）

角度失配，即入射光束没有从光纤端面正入射，如图14所示。

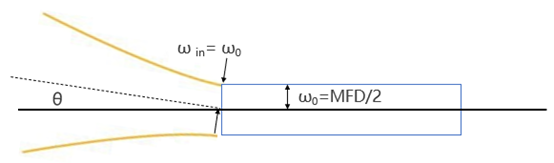
图14：角度失配

此时，假设入射光束的束腰直径等于单模光纤的MFD，入射光束的束腰中心与纤芯中心横向对准，但是，入射光束的束腰与光纤端面的夹角为θ，此时单模光纤的耦合效率为

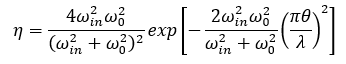
图15为SMF-28单模光纤耦合角度失配的拟合曲线。

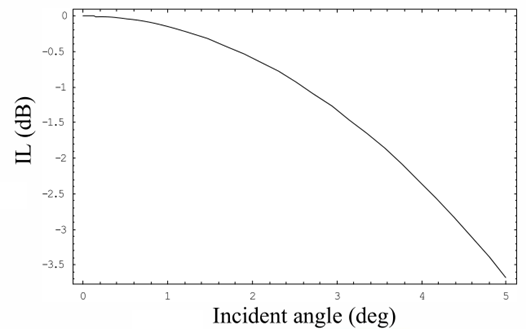
图15：角度失配的拟合曲线

（5）单模光纤失配的一般方程

单模光纤的各种失配情况，如图16所示。

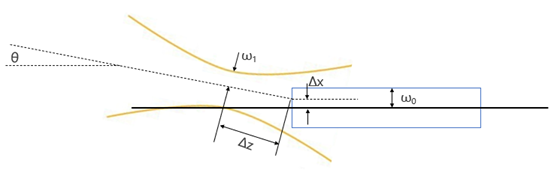
图16：单模光纤的各种失配情况

此时，假设入射光束的束腰直径不等于单模光纤的MFD，入射光束的束腰中心与纤芯中心横向偏移Δx，入射光束的束腰与光纤端面轴向偏移Δz，入射光束的束腰与光纤端面的夹角为θ，此时单模光纤的耦合效率的一般方程为

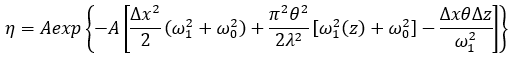
上式中，

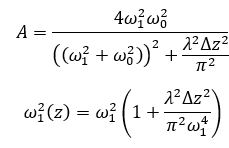
参考资料：

（1）原荣《光纤通信》

（2）陈海涛《光纤通信技术及应用》

（3）Thorlabs索雷博《理解单模光纤》及《关于光纤耦合的五个实用问题》